PLO:零知识证明： Plookup算法介绍_LOOK

作者：

时间：

最近有空看了看Plookup的论文。针对对电路描述不友好的操作（比如bit操作），Plookup给出了新的思路和证明方式。给定某个操作的真值表示（lookup table），证明某个操作的输入/输出是在真值表中。这种方式，相对之前的bit计算约束方式，降低约束的个数，提高了电路效率。

Plookup的论文下载地址如下：

https://eprint.iacr.org/2020/315.pdf

基本思想

Plookup尝试解决的问题是，给定两个集合，证明某个集合的元素在另外一个集合中。给定两个集合t和f，s是f排序后的结果。如果t中的元素最少在f中出现过一次。判别f中的元素是否包括在t中，只需要比较元素差的集合：

多链Web3生态Hacker资助计划Dora Grant DAO首轮零知识投票环节结束:11月14日消息，社区驱动的多链Web3生态开源极客资助计划Dora Grant DAO已于北京时间11月13日23:59在开发者激励平台DoraHacks.io关闭首轮投票通道。投票最终结果和零知识证明文件将于14日晚八时公布。首期20万美金Grant奖金将会根据投票结果的排序进行发放。

Dora Grant DAO计划旨在持续支持在以下三个领域的多链Web3开源极客团队：多链Web3核心基础设施和工具，加密原生应用，加密-前沿科技交叉领域。[2022/11/14 13:01:29]

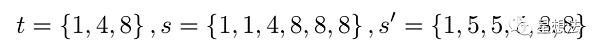
两位数学家因对零知识证明的研究获得数学界大奖阿贝尔奖:据DeepTech深科技消息，近日，备受瞩目的数学界大奖阿贝尔奖公布两名获奖者，一位是匈牙利数学家拉兹洛?洛瓦兹（László Lovász），一位是以色列计算机科学家阿维?威格森（Avi Wigderson）。两位数学家因为对零知识证明的研究，而获此殊荣。曾经让纯数学家看不起的零知识证明，却获得了数学界举足轻重的阿贝尔奖。正如颁奖词所说：“表彰其在理论计算机科学和离散数学方面做出的杰出贡献，以及在将之塑造为现代数学中心领域中发挥的主导作用。”零知识证明比起其他复杂算法更为简单，但这两位数学家对于零知识证明的研究，不仅对现代数学核心计算有重大贡献，还有巨大的现实意义：其一，零知识证明对数字货币的认证意义重大；其二，零知识证明还可以用于人的身份验证，即在不透露密码的前提下，验证方通过一系列问题来让对方提供 “我知道正确密码”，或在信息安全领域，提供 “我就是本人” 的证明。[2021/5/2 21:16:57]

举个例子，t是{1，4，8}的集合，元素的差异集合为{3, 4}，分别是4-1，8-4。如果s只有t中的元素组成，并且每个元素最少出现一次，例如{1，1，4，8，8，8}，元素的差异集合也为{3，4}。如果s中的元素并不完全是t中的元素，那即使在元素差异集合一样的情况下，也不能说明s中元素在t的集合中。例如s为{1，5，5，5，8，8}，元素的差异集合也为{3，4}，分别是8-5，5-1。

动态 | 以色列理工学院教授违反知识产权规定建立零知识证明技术公司:据Bitcoin.com报道，以色列理工学院教授Eli Ben-Sasson因违反了该学校知识产权规定而被起诉。据报道，Ben-Sasson利用在为该机构工作时开发的知识产权建立了一家零知识证明技术公司。Ben-Sasson是区块链技术初创公司Starkware的联合创始人兼首席科学家，以色列理工学院在法庭提出要求Ben-Sasson转让其在该公司的50%股份。[2019/4/23]

论文提出，可以引入一个随机因子，将前后两个元素相加的方法，确定两个集合的依赖关系。

定义多项式

在基本思想的基础上，论文在第三章定义了两个多项式F和G：

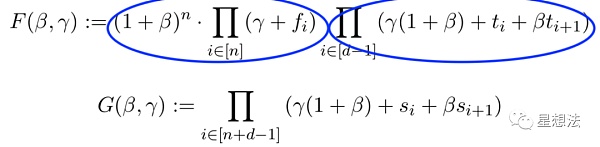
如果F和G相互对等，有且如下的条件成立：

f集合属于t

s是(f，t)的并集，并且按照t中的元素排序

如果条件成立，可以推导出两个多项式相等。F多项式可以看成是两部分组成，分别是两个连乘。后面的连乘可以看成是t中的元素连乘。前面的连乘，可以看成是f中元素的连乘。因为f中的元素属于t，则f中的元素的连乘，可以想象成多个相同元素的连乘。反之，因为beta和gamma的随机因子，也能从F和G对等条件推出满足的两个条件。具体的证明过程，可以查看论文的第三章。

在定义多项式的基础上，问题可以转化成两个多项式相等。

Plookup协议

已知f和t，可以排序得到s。因为s由f和t合并而成，s可以由两个函数h1和h2表示。关键在于第4步，定义了Z函数：

Z(g) = 1 - 初始为1

Z(x) 是两种多项式表示的商

Z(g^(n+1)) = 1 - n+1元素的连乘，两种多项式表达式相等