StarkNet:零知识证明的基础介绍及其在区块链领域的应用_ARKN

在复杂的密码学领域，零知识证明为一项看似矛盾的任务提供了独特的解决方案：在不透露信息本身的情况下证明知道某一信息。这种加密方法涉及两方：证明者及验证者。证明者的目的是证明他们拥有某一信息（我们称之为x），而不透露任何关于x本身的数据。验证者则从交流中了解到的只是证明者拥有这种知识的简单事实。最重要的是，验证者并没有获得关于x的额外信息。

比如当小零与小十在玩密室逃脱，此时小零告诉小十他已经破解了某“宝箱”的密码。但是小零不愿意直接分享现成的“答案”，也不愿当着小十的面将宝箱打开。那么怎样证明给小十，他真的破解了迷题并且知道宝箱密码呢？

于是他让小十在一张纸上写一段只有自己知道的字符串，同时签上自己名字，将纸张从宝箱的缝隙中塞了进去。

随后小零打开宝箱取出了小十放进去的纸张，并展示给了小十看，小十核对字符串和签名无误。这证明了小零确实知道宝箱密码，而且这张纸确实是宝箱里拿出来的。

该解密过程既没有被小十知晓，同时小零又证明了他已破解了宝箱密码。

零知识证明

密码学中，零知识证明（Zero Knowledge Proof，也称ZKP）或零知识协议是一种方法，该方法可令证明者在不透露信息本身或其他任何信息的情况下，让验证者相信或证明给验证者某个陈述或论断的真实性。

多链Web3生态Hacker资助计划Dora Grant DAO首轮零知识投票环节结束:11月14日消息，社区驱动的多链Web3生态开源极客资助计划Dora Grant DAO已于北京时间11月13日23:59在开发者激励平台DoraHacks.io关闭首轮投票通道。投票最终结果和零知识证明文件将于14日晚八时公布。首期20万美金Grant奖金将会根据投票结果的排序进行发放。

Dora Grant DAO计划旨在持续支持在以下三个领域的多链Web3开源极客团队：多链Web3核心基础设施和工具，加密原生应用，加密-前沿科技交叉领域。[2022/11/14 13:01:29]

零知识证明最初是于由麻省理工教授Shafi Goldwasser、Silvio Micali以及密码学大师Charles Rockoff三位作者在《The Knowledge Complexity of Interactive Proof Systems》论文中提出的。该一算法概念为现代密码学奠定了一定基础。

零知识证明有两个额外的属性：简明性和零知识。简明性允许验证者接受一个大型计算的正确性，而无需自己计算该语句或陈述。而零知识保证了没有任何关于输入的数据被泄露。

研究机构Geometry将正式启动并支持采用零知识系统和应用数学的Web3项目:6月28日消息，专注于零知识隐私技术的研究和投资公司Geometry已运营几个月时间，负责人为Aztec Network前首席执行官Tom Walton-Pocock，团队成员还包括Celo密码学负责人Kobi Gurkan和Oiler Network前增长主管Gregoire Le Jeune。Geometry表示，其还获得了由对冲基金经理Alan Howard支持的孵化器WebN Group的孵化。

Geometry已领投以色列零知识半导体公司Ingonyama的400万美元种子轮融资，并领投了对NFT市场流动性项目Soap Labs的200万美元种子轮融资，以及参投了跨链基础设施Socket的种子轮融资。[2022/6/28 1:36:24]

零知识证明对于确保许多加密协议的隐私和安全至关重要。它们是防止潜在信息泄露的保障，是Crypto世界的隐形防弹衣。该知识的应用可延伸至不同领域，包括区块链技术和安全认证系统，其中敏感数据的保护是最重要的。

应用领域广泛

区块链及加密技术：像Zcash这样的区块链技术使用了零知识证明来保护交易隐私。一个人可以证明他们有足够的Cypto货币来进行交易但又不透露其资金的确切数额。这保证了隐私的同时确保了交易的完整性。

a16z宣布推出使用零知识证明技术的空投领取工具:金色财经报道，加密风投机构a16z在官网宣布推出使用零知识证明技术的空投领取工具，使得加密项目方向活跃贡献者发放空投时保护贡献者的地址隐私，特别是根据用户链下活动空投代币的情况下。

具体而言，潜在的空投接收者可以通过公共渠道（如 Telegram、Discord、Twitter 或 Signal）提供消息（称为“承诺”）；然后，空投者通过将这些承诺散列在一起，构建一个Merkle树。随后，潜在的接受者可以通过提供零知识Merkle证明，证明他们是树内承诺的作者，而无需透露是哪一个，从而声称自己的空投份额。

a16z称，以这种方式申领代币将收件人的公共地址与所有其他有权空投的用户的公共地址混合在一起，从而保护他们的匿名性。[2022/3/28 14:21:12]

身份验证及认证：零知识证明还可以在不透露不必要的信息同时，用于确认身份。例如，一个人可以在不提供确切的出生日期的情况下证明他们已经超过18岁，或者在不分享密码等敏感数据的情况下证明他们的身份。这最大限度地减少了盗取身份或未经授权访问的风险。

安全多方计算（SMPC）：零知识证明可以促进多方之间的复杂互动，其中每一方都可以证明他们遵循商定的协议，而不透露其输入的具体内容。这在如保护隐私的数据挖掘、安全投票系统等诸多方面都十分有效。网络安全：零知识证明可以提供改进的安全协议，如安全密码政策。其可以验证用户提出的密码是否符合某些安全标准，而不让服务器知晓或记录实际密码。因为密码不会被储存在任何地方，因此可以防止潜在的违规行为。保护隐私的同时共享数据：零知识证明可以用来证明某些数据符合特定的要求，而不透露数据本身，这在医疗或金融等领域尤其重要。这些领域对数据隐私的规定很严格，但以安全、保护隐私的方式分享信息或许会带来巨大收益，比如促进医疗事业的发展等等。零知识证明已经在区块链中释放了新的技术可能性。这可以从ZKSync和Polygon的zkEVM等各种Layer 2中看到。然而，这仅仅是零知识证明创建的区块链的一个子集。

零知识证明系统Bulletproofs+代码获准可在门罗币协议中使用:12月30日，门罗币发推宣布，零知识证明系统Bulletproofs+的代码现已获得许可，可在Monero协议中使用，以替代现有的Bulletproofs零知识证明系统。新系统将使得门罗交易结构变得更小，钱包交易速度更快以及网络验证速度更快。此外，官方表示，该代码具有功能性并包括对基础算法的测试，若考虑将来在门罗币网络升级中进行部署，则应该由第三方进行审核。[2020/12/30 16:04:23]

如何表示一个证明

在这一节以及文章的其余部分，我们将重点讨论为基于PLONK证明系统构建的证明。

PLONK是一种零知识证明系统，其全称是

“Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge”，即“基于拉格朗日基数的全局非交互式知识证明排列”。

从本质上讲，PLONK是一个通用的、可更新的加密证明系统，这一创新允许在区块链系统和其他分布式网络中进行有效的验证和扩展。PLONK背后的想法是构建一个通用的且可更新的证明系统。在零知识证明系统的背景下，“通用”意味着它可以被用于任何类型的计算；“可更新”则意味着加密参考字符串（用于生成和验证证明的一段数据）可以随着时间的推移安全地更新。

声音 | V神评价MimbleWimble：只有零知识证明 ZK-SNARKs 等全局匿名集，才能真正保证隐私安全:针对 Dragonfly Capital 的分析师 Ivan Bogatyy 发布的关于阐述 MimbleWimble 协议有重大缺陷、Grin 网络 96% 的交易可被破译的文章。

以太坊创始人Vitalik在推特回应称：如果隐私模型设置了一个中等的匿名集，那么它实际上设置了一个小范围的匿名集。如果隐私模型的匿名集较小，则其匿名集为 1。只有全局匿名集（例如，使用 ZK-SNARKs 技术进行的加密）才真正具有安全性。[2019/11/19]

PLONK因其高效和简单性而引人注目，也因此成为了对安全、私密交易系统有需求的项目及公司的热门选择。与其他系统相比，它每个gate（计算的基本单位，我们下文统称“门”）使用的约束条件更少，这使得计算速度更快且可扩展性更高。Vitalik Buterin已经发表了关于PLONK的更全面的描述。[复制下链接至浏览器即可查看原文https://vitalik.ca/general/2019/09/22/plonk.html]证明

在证明某个陈述前，我们先将该陈述用电路表示。一个电路将计算中的值与另外两种类型的数据一起编码：

1. 操作：比如对输入数据进行的乘法和加法计算2. 操作执行的顺序

为了编码这些数据，PLONKish电路会被表示为一组向量和约束条件。约束条件是向量中单元必须遵守的关系，其中约束类型有：门约束和复制约束，他们分别表示电路中的操作和操作的顺序。

采用不同的门和电路架构，有多种方法来表达电路。

将陈述表示为一个电路

假设我们有两个门：一个乘法门和一个加法门。乘法门被表示为一个长度为3的向量|a|b|c|。如果这个门被选中，那么它将约束c等于a*b。同样，加法门表示为一个长度为3的向量，如果选择加法门，则c等于a+b。使用这些门，让我们表示两个向量（a,b）和（c,d）之间的点积。要做到这一点，我们需要完成以下计算：1. 使用乘法门计算a*b2. 用乘法门计算c*d3. 用加法门计算ab+cd这可以用向量来表示。

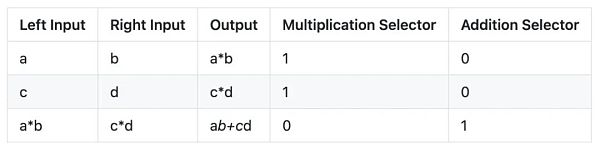
注意，第一个和第二个乘法门的输出是加法门的输入值。这个数据在我们的电路中是和门的约束条件分开编码的。这被称为复制约束。那么，为什么电路约束很重要呢？如果没有约束，那么恶意验证者就可以在电路中输入他们喜欢的任何数值。例如，验证者可以用aba*b替换ab+cd。与智能合约类似，约束条件在使用前必须通过证明系统得到验证。证明陈述

现在我们可以用电路来表示陈述，那么证明者如何说服验证者证明是有效的呢？对于PLONK系统来说，证明者必须让验证者相信门的约束和复制约束得到了实现。对于复制约束来说，这是通过进行排列组合检查来实现的。

替换检查是由Bayer-Groth首先提出的，然后由Gabizon、Williamson和Ciobotaru在PLONK论文中得到了进一步发展。为了证明门的约束，需要计算某个quotient polynomial（商的多项式）。

直观地说，置换检查表明，如果复制约束的条目被置换，电路仍然是相同的。置换检查

如果对于b的所有第i个位置，存在与a相等的σ(i)位置，我们就说一个矢量a与矢量b之间是通过置换σ来关联的。我们将其表示为σ(a)=b。给定两个向量a=(a,b,...,c), b=(a',b',...,c')$, 和置换σ，我们想确定σ(a)=b。这可以按以下方法进行：

将向量表示为a'=((a,1),(b,2),...,(c,n))和b'=((a',σ(1),(b',σ(2)),...,(c',σ(n)) )。这是对关于置换σ的向量进行编码。

将向量重写为多项式向量：a''=((a+1X),(b+2X),...,(c+nX))和b''=((a'+σ(1)X), (b'+σ(2)X),..., (c'+σ(n)X))

检查a''和b''作为多集是否等价，可以通过随机选择gamma来完成，从而显示$(a+1X+γ)(b+2X+γ)....(c+nX+γ) = (a'+σ(1)X)+γ)(b'+σ(2)X+γ)....(c'+σ(n)X+γ)$ 。

通过随机选择一个β，我们可以通过Schwartz-Zippel lemma检查这些多项式是否等价。如果它们作为多项式是等价的，那么集合a''和b''作为多集则是等价的。如果它们不是等价多项式，那么a''和b''就不是等价的多集。

CertiK中文社区

企业专栏

阅读更多

区块律动BlockBeats

曼昆区块链法律

Foresight News

GWEI Research

吴说区块链

西柚yoga

ETH中文

金色早8点

金色财经 子木

ABCDE

0xAyA

标签：ARKNSTAStarkNetRKNstarknet币价分析stader币币RKN币

PEPE热门资讯