PLO:【密码专栏】超强进阶：PLONK VS Groth16（上）_RTE

前言

前文《天冷了，干了这碗“零知识证明”鸡汤》对「零知识证明学习」作了一个形象化的比喻：炖鸡汤。那么本系列的主要内容可以简单概括为《论高压锅炖鸡汤的一百种方法》之方法二。在学会了“清炖鸡汤”之后，不如来一口“阿胶鸡汤”补补脑细胞吧！

正如鸡汤不同风味之间各具千秋，不同的zk-SNARK方案也各有所长。zk-SNARK方案可以被分为与zk-SNARK，PLONK与Groth16分别是其中的典型代表。通过本系列，我们将对PLONK算法内容作简要介绍，并指出PLONK和Groth16算法思路上的异同。

PLONK算法在中提出，由来自于ProtocolLabs的研究员Gabizon和以太坊隐私交易协议AztecProtocol的两名研究人员合作完成。PLONK的提出晚于Groth16，在证明和验证的性能上与Groth16也存在一定差距，但是基于通用可更新的可信设置这一特点，使PLONK算法在零知识证明领域占据了一席之地。

可信设置

可信设置可以说是PLONK和Groth16两者间最显著的差异。正是为了避免一次性的可信设置，PLONK设计了后续的约束系统和问题压缩方式。那么什么是零知识证明中的可信设置呢？可信设置实际上是在创建一个用于证明验证的秘密，任何知道这个秘密的人都可以伪造证明通过验证。如果将零知识证明看作是一扇挡在证明者a和验证者b之间上锁的门，那么合法构建的证明就是可以打开门的口令，a提供口令即可进入房间。但是如果a得知了门的秘密也就是房间窗户的位置，那么a可以直接无视锁的存在翻窗进入房间。

两巨鲸地址向Binance存入约370万美元PENDLE:7月3日消息，据Spot On Chain监测，两巨鲸地址向Binance存入大量PENDLE。0x554开头巨鲸地址在休眠284天后，于30分钟前向Binance存入其全部218.8万枚PENDLE（约 253 万美元）。0xa9e开头巨鲸地址于20分钟前向Binance存入100万枚PENDLE（约117万美元）。[2023/7/3 22:15:07]

▲无窗的房间

显然，最安全的做法是找一个「没有窗的房间」，这也是一部分零知识证明方案的思路——无需可信设置，例如可扩展透明知识论证zk-STARKs和防弹证明Bulletproofs。虽然它们的安全性得到提高，但是目前这类方法的证明验证性能是远低于zk-SNARKs的，近线性的验证和规模较大的证明使其不适用于很多场景。

▲窗户位置指定策略

PLONK和Groth16的做法都是保留窗户，但是尽力保护窗户的位置不被别人知道。

Groth16的做法是：根据不同的问题，每次都指定窗户在房间中的摆放位置，也就是它需要一次性的可信设置。而PLONK面对不同的问题时：窗户的位置是固定不变的，即窗户的位置只需要被指定一次。也就是说PLONK的可信设置是通用的。那么这些窗户指定的位置由谁来确定呢？当然，可信第三方是一个备选项。但这意味着说这间房间是否会被恶意证明者攻破，其安全性寄希望于这位第三方。除此之外还有一项热门技术也可为其提供思路——多方安全计算。沿用之前的例子，可以不太严谨地将MPC概括为：多个人共同指定窗户的位置，除非这些参与者全部联合起来对答案，这个位置将无法由任何人得知。

数据：链上前五位ARB买家购入总计逾1300万枚ARB:金色财经报道，据Lookonchain统计，链上ARB前五位巨鲸买家以1.28至1.38美元的单价购入总计逾1300万枚ARB，其中，l0xb154开头地址以3,700枚ETH（679万美元）购买了494万枚ARB，购买单价为1.38美元。0xb0fc7开头地址用352万USDC购入274万枚ARB，购买单价为1.28美元，该地址通过在Uniswap上为ARB提供流动性已赚取177万美元的交易费用。

另外，0x139e3开头地址用356万枚USDC和USDT购入261万枚ARB，购买单价为1.36美元；0xf53fe开头地址用195万枚USDC购入153万枚ARB，购买单价为1.28美元。0xa161a开头地址用199万USDC购入149万枚ARB，购买单价为1.33美元。[2023/3/24 13:24:05]

显然，使用MPC时，参与者的数量越多，秘密的安全性越高，这类可信设置也比可信第三方更为用户所接受。遗憾的是，虽然目前提出了基于Groth16的可信设置，但是由于Groth16的秘密计算与特定的问题相关联，每次遇到新的问题时，必须重新开启一轮MPC可信设置。可想而知，需要多方参与的计算协议将是极为繁琐的，这样将大大影响Groth16的性能。相比之下，具备通用性的PLONK与MPC的适配度极高。

路透社：截至11月20日FTX现金余额总计为12.4亿美元:11月22日消息，据外媒报道，根据周一提交给法院的文件，截至11月20日，已申请破产的加密交易所FTX的现金余额总计为12.4亿美元。文件称，到12月23日，FTX的现金流将从11月25日的4.79亿美元减少2000万美元，至4.59亿美元。

此前11月20日消息，FTX欠前50名最大无担保债权人共31亿美元。（reuters）[2022/11/22 7:56:12]

而之前提到的PLONK可信设置的可更新性则是指：通用的PLONK秘密可以通过再开启一轮MPC作更新。新生成的秘密安全性建立在两次MPC的安全性上，只要两次中有一个参与者是诚实的，这个秘密就是可信的。约束系统

Groth16及PLONK均将程序先转化为一个由加法门和乘法门组成的算术电路，再通过将电路构建为多项式的形式来进行后续的计算。本节我们将使用Vitalik文章中的一个简单例子进行说明：

对于程序qeval,prover需要证明自己知道qeval(x)=35的解，即x=3。

defqeval(x):

y=x**3

returnx+y+5，其转化为算术电路可表示如下：

FTX已在Kroll开启债权人信息登记，最大单笔索赔金额超1100万美元:11月21日消息，加密交易平台FTX已在美国公司调查和风险咨询公司Kroll的平台上开启债权人信息登记页面，当前最大单笔索赔金额为ETHEREALTECHPTE.LTD.登记的11,690,000美元。

此前报道，11月18日，FTX Group现已聘请Kroll作为其索赔代理人，所有向美国破产法院提交的官方文件均可在cases.ra.kroll.com/FTX/查询。[2022/11/21 7:51:57]

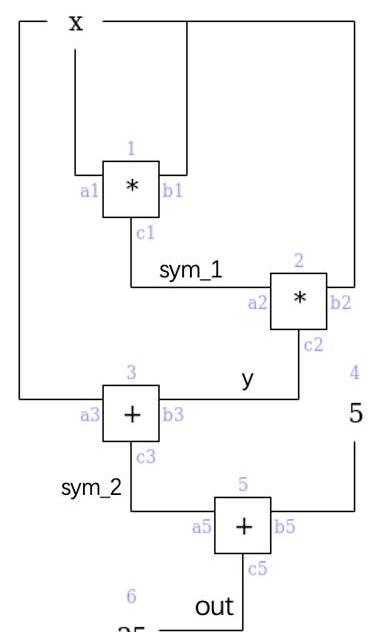
PLONK中，上图电路的描述由两部分组成：门约束与线约束。门约束固定电路中每个门的动作。此外，在电路中我们规定相连线的值应保持一致，对此线约束规定这些线的关系。接下来我们分别讨论两类约束的多项式表示。门约束

在PLONK中，对于第i个门，可被描述为如下形式：

（QLi)ai+(QRi)bi+(QOi)ci+(QMi)aibi+Qci=0

其中Q均为常数，a,b,c则是信号的下标。具体地，在PLONK中门约束可以被分为三类：算术约束、布尔约束、公共输入约束。

最为常见，用于表示电路中的所有加法门和乘法门，此时a,b,c分别表示门的左右输入和输出信号下标，Q_C一般为0。根据门的类型剩余的符号有不同的取值：

加法门：QLi=1，QRi=1，QOi=-1，QMi=0??ai+bi-ci=0乘法门：QLi=0，QRi=0，QOi=-1，QMi=1-ci+?aibi=0

顾名思义，用于约束布尔类型的信号，其值只能取0或1。例如现在需要约束下标为j的信号∈{0,1}，那么门约束式子中各变量的取值为：

ai=bi=j，QLi=-1，QMi=1，QOi=QRi=Qci=0

-j+j*j=0

另外，针对问题中出现的证明方和验证方都知道取值的输入，需要在约束系统中有所体现。例如要求约束下标j的信号取值为v，对应的取值为：

ai=j，QLi=1，QMi=QOi=QOi=0，Qci=-v

j-v=0

利用该式，我们可以很容易地表示上图中的所有门约束：

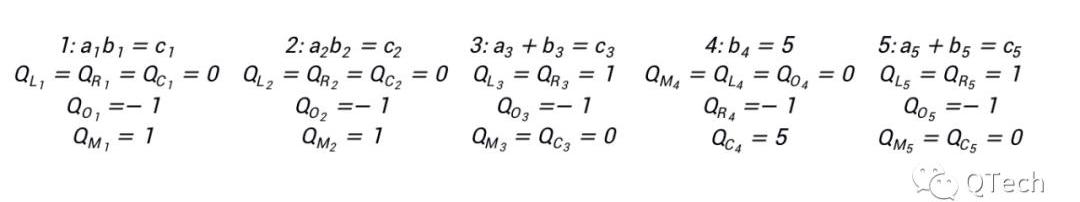
与Groth16类似，可以将所有的多项式组整合在一个多项式中：

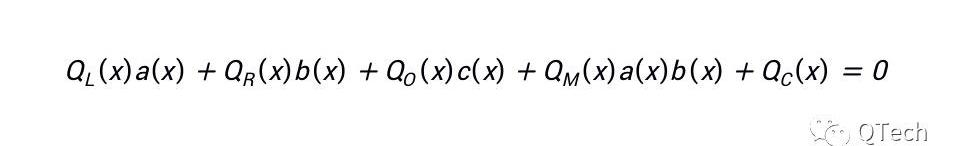
线约束

线约束可以分为两种情况：

同一多项式内部，例如：a1=a3

不同多项式之间，例如：a1=b1

当只需要考虑情况1时，可以通过构造p(x)=P(x)来实现约束：

X(X)=X

p(X+1)=p(X)*(β*X(X))+Y(X)+γ）

P(X+1)=P(X)*(β*X(σ(X))+Y(X)+γ）

p(0)=P(0)=1

其中β,γ为随机数，X->Y表示了待约束的多项式，P(x)使用了x的置换σ(x)。对于下面例子：

X(1)→Y(1)

X→Y：X(2)?→?Y(2)?and，Y(1)=Y(3)

X(3)→?Y(3)

σ(1)=3

σ(X)：σ(2)=2

σ(3)=1

当且仅当Y(1)=Y(3)成立时，p(x)=P(x)。

现在，让我们增加问题的复杂度：需要约束的多项式个数为k时。自然地，设门的总数为n，我们可以对第j个多项式构造对应的p_j(x)=P_j(x)，即

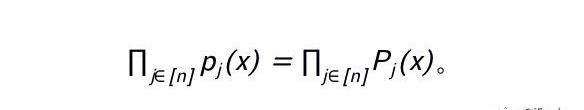
进一步地，情况2的出现要求对以下情况中的x作区分：

pj(x)and?pi(x)????

那么可以增加对x的映射，对于第j个多项式：

X(X)=(j-1)*n+X

p(X+1)=p(X)*(β*X(X))+Y(X)+γ）

P(X+1)=P(X)*(β*X(σ(X))+Y(X)+γ）

p(0)=P(0)=1

以上就是线约束的全部内容，其实质是为了保证电路中同一条或相连线上的值相等。

与Groth16类似，将上述的约束联立将得到一个完整的PLONK约束系统。通过将抽象的代码和电路转化为约束系统R1CS，我们可以将一个零知识证明问题固定下来。让我们带着问题进入下篇：PLONK中如何将R1CS转为多项式描述？它与Groth16做法区别在何处？敬请期待！

ArielGabizonandZacharyJ.WilliamsonandOanaCiobotaru.(2019).PLONK:PermutationsoverLagrange-basesforOecumenicalNoninteractiveargumentsofKnowledge.

SeanBoweand?ArielGabizonandIanMiers.(2017).ScalableMulti-partyComputationforzk-SNARKParametersintheRandomBeaconModel.

https://vitalik.ca/general/2019/09/22/plonk.html

标签：NFTPLORTEORTUNFT币PLOCK币CARTELBSHORT价格

火币下载热门资讯