AIN:科普 | 天冷了，干了这碗“零知识证明”鸡汤_GRO

前言：从一锅鸡汤说起

当读者刚开始接触零知识证明的概念时，面临第一关就是如何搞懂突如其来的大量名词，比如离散对数问题、双线性对还有Groth16、PLONK、RedShift等。不妨我们借用“烹饪”这个生活场景来类比其中的层次关系。

如果把“密码学”比做“烹饪”，那么上个系列中对双线性对的学习就类似于学习炖汤前先简单了解的高压锅的工作原理，而zkSNARK则相当于在说明如何用高压锅炖出美味鸡汤。

由此可见，双线性对是类似基础工具的角色：就像高压锅既可以炖鸡汤也可以炖排骨汤，双线性对既可以用于零知识证明也可以用于构造签名等密码学算法。而Groth16、PLONK、RedShift等，它们同属于zkSNARK，属于同一层次，如果沿用上述类比，那大概就是对应用高压锅做汤的风味选择了。Groth16算法是JensGroth提出的一种zkSNARK算法，相关论文不仅对已有算法进行改进，而且讨论了基于配对的非交互式零知识论证的证明大小问题。Groth16因其精简的证明大小和高效的验证效率，在ZCash等项目中多有应用，是最经典的零知识证明算法之一。

徐明星新书《趣说金融史》正式发布 科普金融发展之道:金色财经现场报道，9月23日，欧科云链创始人徐明星携手著名财经作家李霁月、行业观察者顾泽辉力作《趣说金融史》一书，跨越5000年金融历史，重读金钱故事，并预测新的金融时代。该书由中信出版社出版，将于近期正式发售。据了解，本书可以更好地呈现金融的起源与发展，帮助人们理解货币、金融与未来经济。作为区块链行业领军企业——欧科云链的创始人，徐明星深知技术探索对经济社会的重要推动作用，他曾先后出版过《图说区块链》、《区块链：重塑经济与世界》、《通证经济》、《链与未来》等行业权威著作，解读区块链等新型技术的推动下，金融与社会的升级之道，对经济社会发展做出了重大贡献。其中，《区块链：重塑经济与世界》曾作为新中国70周年重点推荐图书之一被相关书店推荐。[2021/9/23 17:00:57]

上一个系列中我们完整介绍了零知识证明中用到的椭圆曲线和双线性配对相关的基础知识。本系列通过动手算的方式，以Groth16算法为例，循序渐进地介绍zkSNARK的基本原理。

国务院：推进科普与区块链技术深度融合:为贯彻落实党中央、国务院关于科普和科学素质建设的重要部署，依据《中华人民共和国科学技术进步法》、《中华人民共和国科学技术普及法》制定《全民科学素质行动规划纲要（2021－2035年）》，其中要求实施智慧科普建设工程。推进科普与区块链等技术深度融合，强化需求感知、用户分层、情景应用理念，推动传播方式、组织动员、运营服务等创新升级，加强“科普中国”建设，强化科普信息落地应用，与智慧教育、智慧城市、智慧社区等深度融合。（新华社）[2021/7/10 0:40:52]

本篇是“动手算Groth16”的上篇，主要介绍如何从程序转化为电路和描述算数电路的一种约束系统R1CS。下篇会介绍如何从R1CS转化为多项式相关的约束问题，并且详细给出完整的Groth16从头到尾的手算步骤。

程序与电路

初始接触通用零知识证明算法时，读者可能最容易感到疑惑的地方就是各种资料中频繁提到的“电路”一词。这里的“电路”是指什么？它又如何等价地对同一个问题进行描述呢？回答这些问题最简单的方式就是使用具体的一个算法例子进行说明。比如我们有下面一段程序代码，如何将其转化为等价的电路呢？

欧科云链集团正式启动区块链科普行动“星途计划”:欧科云链集团于4月26日，正式宣布启动了区块链科普行动——“星途计划”，行动包括将在全国范围展开系列沙龙，加大力度推进区块链科普进机关、进国企、进校园等，联合政府部门、行业协会等共同构建起更加完善和有效的区块链科普教育生态，与此同时，直击区块链科普现存痛点，推出简单易懂的“秒懂区块链”公益短视频课。

该计划旨在全维度推动社会建立对产业更清晰的认知，与“鲲鹏计划”一道助力数字经济及区块链产业本身健康发展夯实“人才”和“产业认知”两大基础。[2021/4/26 20:59:37]

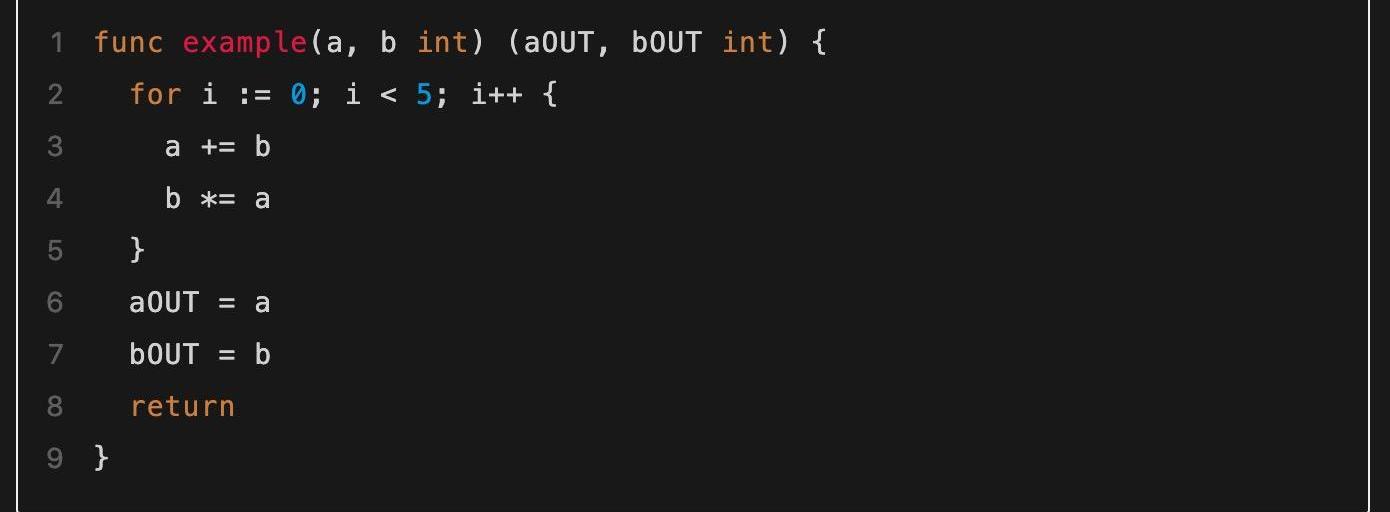
▲需要被转化为电路的代码

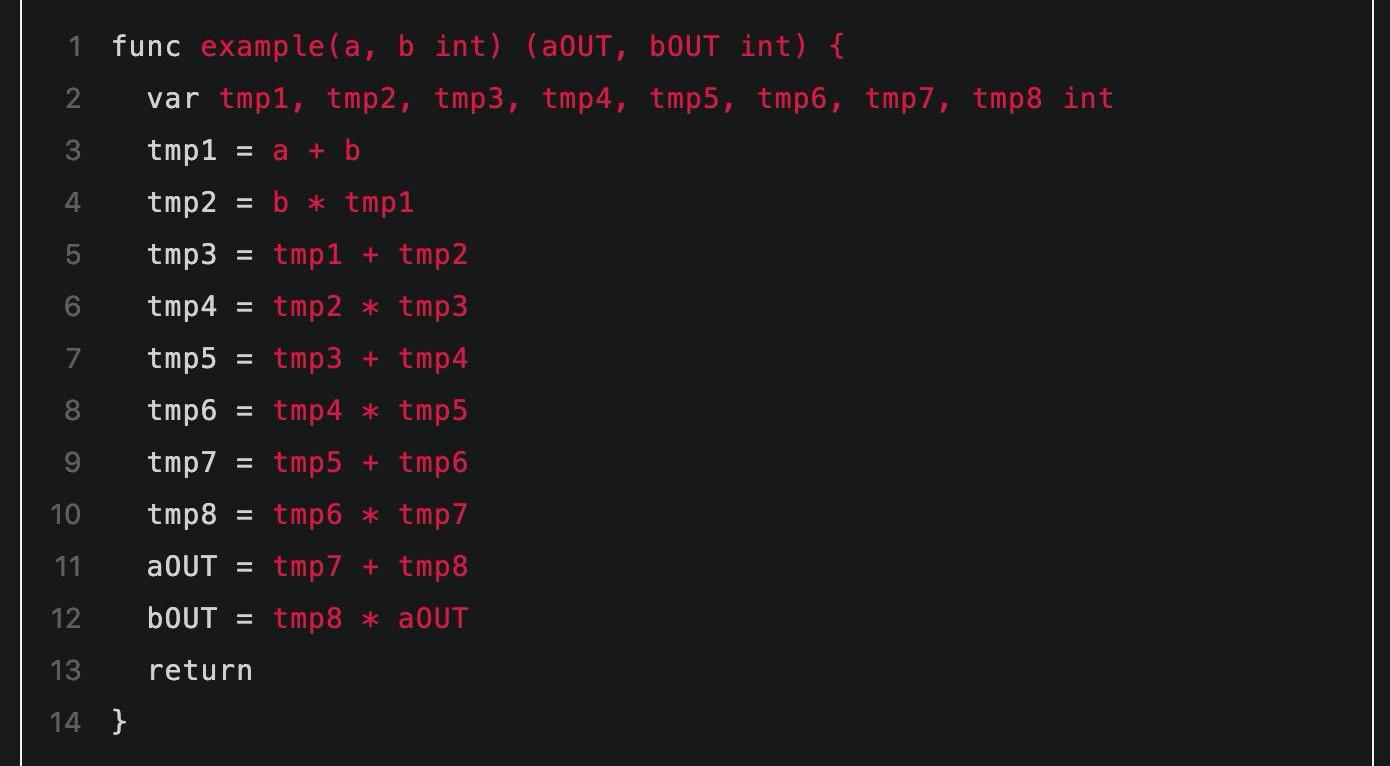
这里需要注意到程序中值被存储在变量中，而电路中的值是用电路门之间的连线表示的。这其中有个关键的不同是：变量的值是会随着时间变化的，而电路中连线的值是固定不能改变的。因此首先我们通过引入一些中间量的方式表示随循环而不断变化的各阶段的变量值，中间量命名为tmp1,tmp2...这样的形式：

人大附中物理老师李永乐科普拜占庭将军问题和区块链:5月14日，人大附中物理老师、科普视频网红李永乐在其公众号发布视频《拜占庭将军问题是什么？区块链如何防范恶意节点？》。李永乐老师在视频中对拜占庭将军问题和区块链进行了讲解，他表示，拜占庭将军问题本质上指的是，在分布式计算机网络中，如果存在故障和恶意节点，是否能够保持正常节点的网络一致性问题。在近40年的时间里，人们提出了许多方案解决这一问题，称为拜占庭容错法。例如兰波特自己提出了口头协议、书面协议法，后来有人提出了实用拜占庭容错PBFT算法，在2008年，中本聪发明比特币后，人们又设想了通过区块链的方法解决这一问题。区块链通过算力证明来保持账本的一致性，也就是必须计算数学题，才能得到记账的权力，其他人对这个记账结果进行验证，如果是对的，就认可你的结果。与拜占庭问题比起来，就增加了叛徒的成本。[2020/5/14]

声音 | 浪潮集团云南分公司总经理：云南区块链产业发展需从“科普”到“专精”不断深化:据昆明日报消息，浪潮集团云南分公司总经理郑昕表示，云南区块链产业发展需从“科普”到“专精”不断深化。下一步，浪潮将继续加大云南农业产业高质量发展体系建设力度，重点以普洱茶等云南优势产业为切入点，打造云南“绿色、有机农产品高地”的品牌形象，并在此基础上，开展基于区块链的供应链金融服务，解决中小企业贷款难、贷款贵问题。[2019/11/11]

▲引入辅助的中间量

最后我们可以转化为只有加法门和乘法门的算数电路：

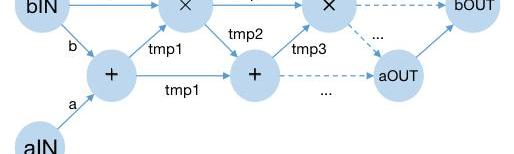
▲电路示意图

这里除去输入和输出外，其他的圆圈代表了电路中的门：可以是乘法门或者加法门。而门和门之间的连线对应了程序中的中间变量在某个时刻的值。

如果站在更高的角度思考，其实可以发现有很多结构都能实现“运算”功能，比如说神经元组成的人脑，比如冯·诺伊曼结构的计算机，甚至更早的机械计算器和当今的人工神经网络。算数电路也是这样的一种能够完成一定运算的结构，而且基于这种结构我们能够完成对计算输入和过程的“零知识证明”。因此通用零知识证明算法普遍引入了“电路”这个运算结构并且会研究，如何更好的将高级语言描述的问题转化为等价的算法电路。

上面例子中约束较多，会给后续的“动手算”产生较多的计算量压力，因此在下文中我们以一个新的例子重新展示这个转化的过程。本系列后续文章都会以这个新的例子为主线进行叙述，从而真实展示证明和验证的具体计算过程。新例子的程序代码如下：

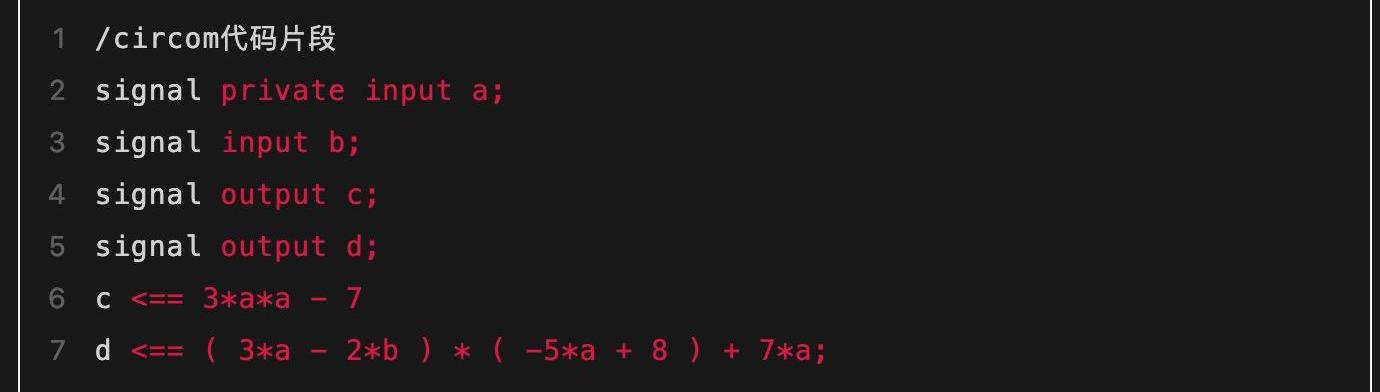
这里涉及到4个连线以及两个等式关系。这两个等式关系用更规范的方式重写一下可以帮助读者看地更清晰：

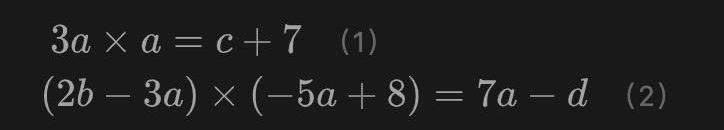
观察这两个式子的特点，可以发现两个等式关系其实都可以写作A×B=C的形式，其中A、B和C都是变量的“加权组合”。这并非巧合，而是我们有意为之。通过这种形式我们避免了对加法门的约束产生额外开销，而是在对乘法门进行约束的同时零开销的对加法关系进行约束，这是groth16的特点之一。在Groth16算法中，加法门和乘法门的地位并不是等价的，我们更关心乘法门。

下面对a,b,c,d四个变量赋予编号，以便下一步的处理,按照groth16的习惯我们将输出排列在输入之前：

可以看到除了连线a、b、c和d，还有一个特殊的连线“1”，“1”其实可以看作是一个特殊的公共输入，他的存在让我们在算法中能更容易地处理常量。“1”的值总是1。

从电路到R1CS

本部分之前先回顾一下向量的内积概念，向量的内积是从两个同维向量得到一个标量的运算，其几何意义对应了“投影”这个概念。比方说两个二维向量的乘法：

·=2×4+3×1=11

回过头看刚才的结果，因为A×B=C这个形式的存在，我们其实能够进一步的对这些等式关系进行抽象。抽象的目的是为了方便编程处理和下一步的讨论。以式子(2)为例，我们其实可以认为他是如下的形式：

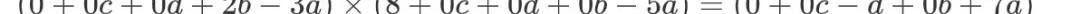
根据上面介绍的向量内积，可以发现这里的A，B，C其实都是向量内积的形式:

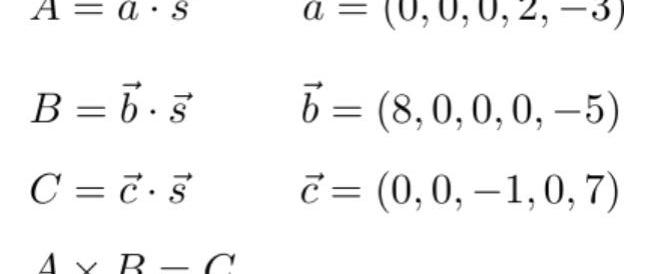
这里的s其实就是全部的连线的值，如果证明者P是真的计算过这个电路的，则P能够获知s的值，否则P无法得知s的值。我们将这个s称为witness。因此通过上面的向量a,b,c我们就能够对s进行一定的约束，即s应该满足：

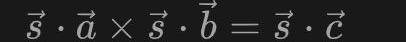
这就构成了一个一阶约束,这样的一个约束对应了电路中的一个乘法门。如果我们将所有的约束联立起来，就得到一个一阶约束系统。通过R1CS我们可以更方便的形式化描述一个零知识证明问题，从而为我们后续解决该问题提供了条件。

下篇我们会介绍如何将R1CS描述转换为多项式描述，并且通过完整的计算过程展示groth16算法的相关内容，敬请关注。

标签：区块链ROTGROAIN区块链技术通俗讲解中山大学ProtonAvocado Blockchain GroupOraichain Token

中币交易所热门资讯