LON:学习笔记 | 零知识证明算法之PLONK——电路_ARK

最近研究了下零知识证明算法-PLONK。肚子里的墨水又增加了，记一下学习成果与新的体会，和大家共同学习---江小白。

现状

近些年，各种新的零知识证明算法层出不出，各有各的特点，各有各的优势。借用V神系列文章里的一张图来简单呈现下当前的零知识证明算法现状。

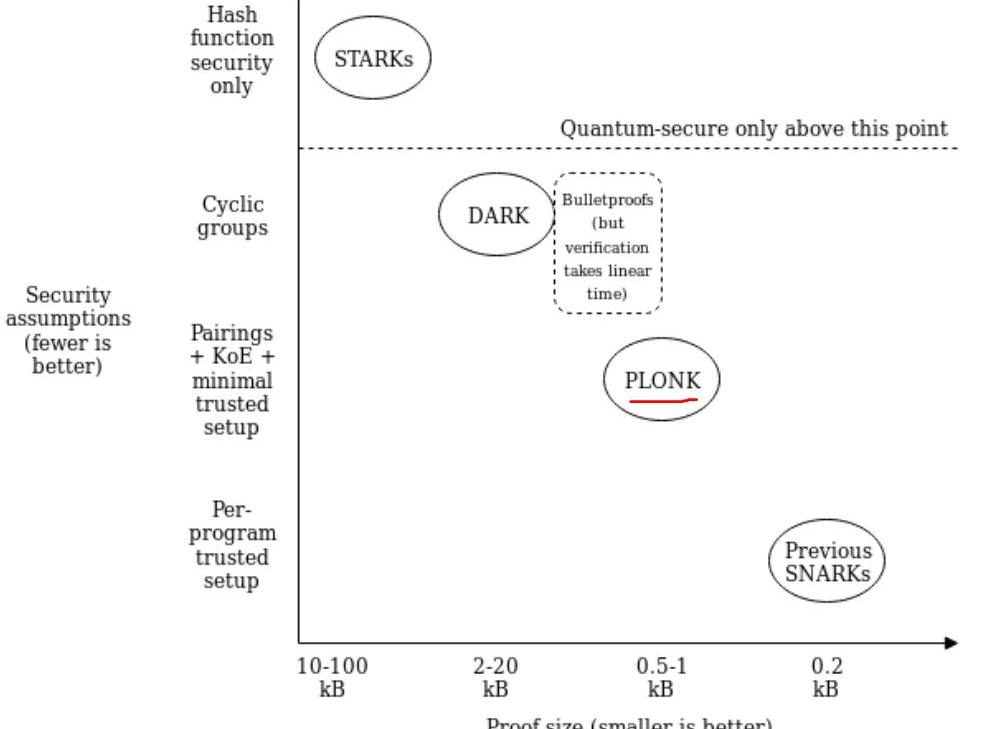
从图中可以简单总结出以下几点：

理论上安全性最高的是STARKs算法，不依赖数学难题假设，具有抗量子性；Proof大小上最小的是SNARKs算法，如Groth16;PLONK算法在安全性上和Proof大小上，位于上述两者之间；其他的这里不做过多阐述，如想了解零知识证明更多信息，可参考链接；对于SNARKs算法，绕不开的一个点就是中心化的TrustSetup，也称之为CRS(theCommonReferenceString)。而无论是PGHR13,Groth16,还是GM17算法，它们的CRS都是一次性的，不可更新的。即，不同的问题将对应着不同的CRS，这在某些场景下，会变得比较麻烦。这些存在的问题，变成了PLONK，SONIC这类算法的一个优势，它们算法虽然也需要中心化的可信设置，但是它的CRS具有一定的普适性。即，只要电路的大小不超过CRS的上限阈值，一些证明问题就可以共用一个CRS，这种CRS称之为SRS(universalStructuredReferenceString)，关于SRS的定义，详细的可参考SONIC协议里的第3小节。PLONK算法继用了SONIC算法的SRS的思想，但是在证明的效率上，做了很大的提升。接下来，让我们详细的介绍下PLONK算法的具体细节，主要从下面四个小节去分享：

ConsenSys推出学习模拟平台MetaMask Learn，以帮助用户了解Web3:金色财经报道，ConsenSys宣布推出学习模拟平台MetaMask Learn，以帮助用户在web3和自我托管钱包的世界中自我定位。据悉，MetaMask Learn是一个免费平台，支持有10种语言，将提供一个交互式的MetaMask UI环境，以帮助那些刚接触自我托管的人，并指导用户使用最常用的功能以帮助他们开始了解web3。[2023/2/1 11:39:27]

电路的设计--描述PLONK算法的电路的描述思想；置换论证或者置换校验--复制约束，证明电路中门之间的一致性；多项式承诺--高效的证明多项式等式的成立；PLONK协议--PLONK协议剖析；电路

PLONK算法电路的描述和SONIC算法一直，具体的过程可以参考李星大牛的分享，已经写的比较详细且易懂。在这个小篇幅里，我想主要分享下我自己的两点想法：

无论是什么样的电路描述方式，电路的满足性问题都要归结于2点，门的约束关系和门之间的约束关系成立；在SNARKs系列的算法里，电路的描述单元都是以电路中有效的线为基本单元，具体的原理可以参考我之前分享的文章，而在PLONK，SONIC以及HALO算法里，电路的描述单元都是以门为基本单元。这两种电路的不同描述方式带来了一定的思考。那就是，之前在研究SNARKs算法时，我们都已经相信一个事实，“多项式等式成立，就代表着每个门的约束成立”，然后推断，整个电路逻辑都是成立；在这个过程中，并没有额外的去证明门之间的一致性成立；但是在PLONK算法里，除了要证明多项式等式成立外，还要额外的用置换论证的数学方法去证明门之间的约束关系，即复制约束。为何会有这样的区别？希望有心的读者能一起在评论区探讨这个问题？我个人理解是因为电路的描述方式的不同：

网易“猪厂学习鸡”发布数字藏品:2月7日消息，由网易人力资源部建立的用于分享学习的公众号“猪厂学习鸡”发布限定款Uniquer系列藏品，包括限时领取的“千鸡千面”的新年flag盲盒（典藏款）和限量发放的学习鸡周边藏品（vip限定）。

据悉，每款藏品每人能且仅能收藏一份，作品版权归猪厂学习鸡所有。收藏后，用户可以永远在网易区块链上查看个人藏品信息。[2022/2/8 9:36:36]

PLONK算法里，电路描述的单元是门，它为每个门定义了自己的L,R,O，因此需要证明门之间的一致性；SNARKs算法里，电路描述的单元是线，门与门之间的值用的是同一个witness，因此不用额外证明一致性；置换论证

前面我们说过，在PLONK算法里，需要去证明门之间的约束关系成立。在做具体的原理解释之前，我们先简单的过一下PLONK协议的过程，如下图所示：

可描述为：

根据电路生成三个多项式，分别代表这电路的左输入，右输入，输出；利用置换校验协议，去证明复制约束关系成立；步骤3和4，校验门的约束关系成立。其中第1点已经在电路小节里阐述过了，接下来，将详细的讲解多项式置换校验的原理。先从简单的场景去讲解：

亿万富翁Mark Cuban：上市公司应学习比特币货币政策，永不发行新股:12月28日消息，达拉斯小牛队老板、亿万富翁Mark Cuban赞扬比特币货币政策称，上市公司应该从比特币中吸取教训，承诺永不发行新股。他们的股票价格会立即上涨。此前消息，Mark Cuban已改变其早前“讨厌”比特币的立场，进而转向推广比特币。[2020/12/28 15:50:43]

单个多项式的置换校验

其实就是证明对于某个多项式f，存在不同的两个点x,y，满足f(x)=f(y)。下面来看具体的原理：

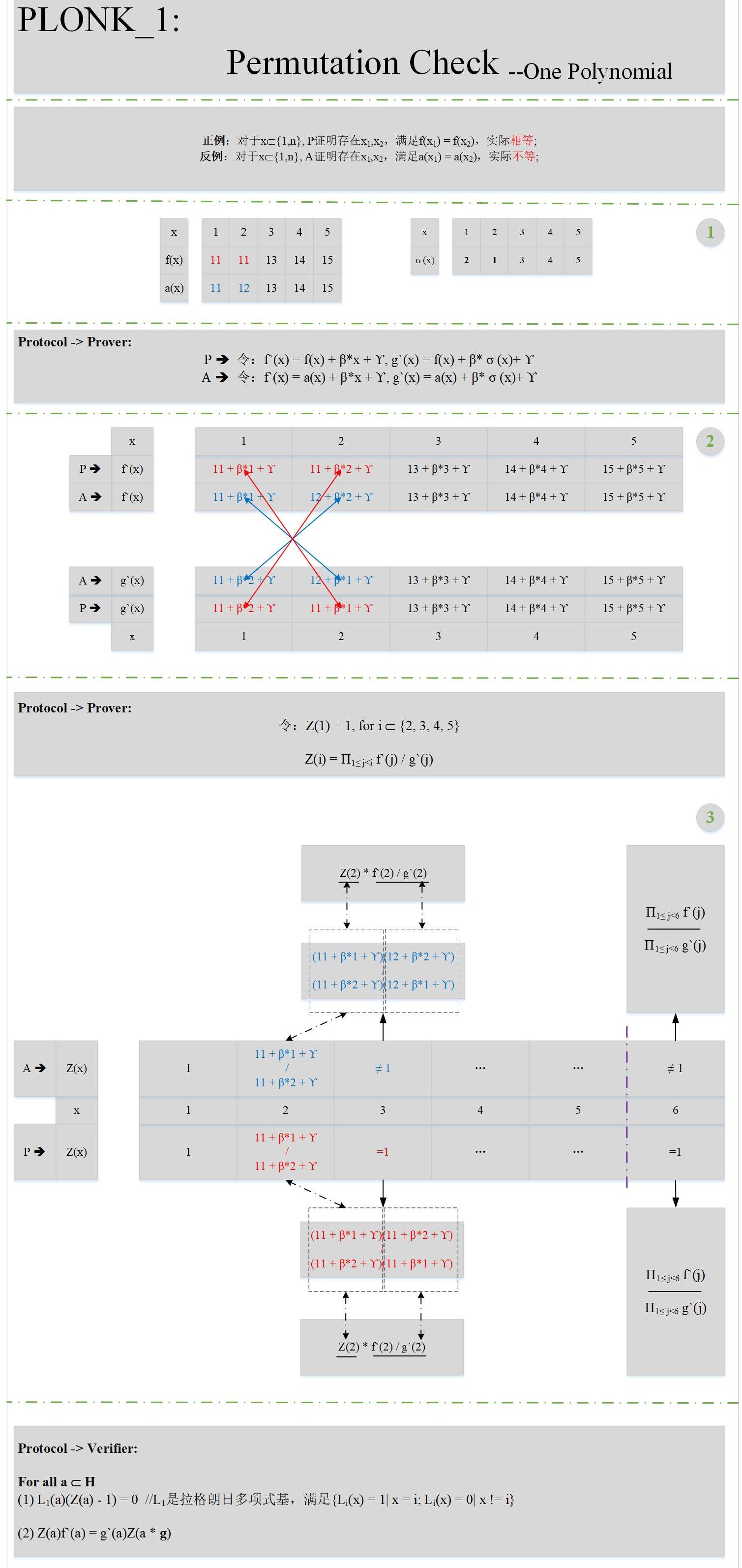
上图中加入了一个正例P，一个反例A，方便大家理解置换校验的原理。有几点需要解释的是：

而经过仔细剖析Z的形式，不难发现，Z(n+1)其实就是两个函数所有值的乘积的比值(不知是否等同于V神文章里的坐标累加器？)。理论上是等于1。因此，我们需要设计这样的一个多项式Z，需满足：deg(Z)<n

动态 | 吉尔吉斯斯坦国家银行或将学习蒙古创建加密货币的经验:据AKIpress今日消息，吉尔吉斯斯坦国会议员Akylbek Japarov建议吉尔吉斯斯坦国家银行学习蒙古在创建其加密货币方面的经验，并提出有关在吉尔吉斯斯坦进行加密的可能性的报告。[2019/12/25]

Z(n+1)=1

2.乘法循环群刚好可以满足这个条件，如果设计一个阶为n的一个乘法循环群H，根据群的性质可以知道Z(g)=Z(g^(n+1))。因此，在设计Z时，会保证Z(g)=1；上图中的自变量的取值也将从{1...n}变成{g...g^n}。所以在上图中验证的部分，a其实已经换成了群H里的所有元素。

3.根据论文中的协议，多项式Z是会发给可信第三方I验证方V会从I处获取到多项式Z在所有a处的取值，然后依次校验。

下面具体看一下论文中的定义：

从定义中可以看出：多项式f,g在范围内具有相同的值的集合；下面看一下论文中具体的协议部分，结合上述解释的3点：

动态 | 美国儿童理财知识杂志创造“比特侠”帮助儿童学习比特币知识:今日微博网友“BTC狂热”发微博称：“美国为方便小朋友学习比特币，设计了比特侠”，并附上相关图片。图片显示，美国儿童理财知识杂志《YOUR$》（financial literacy for kids）（October 2018 Vol.5 NO.2）封面刊登其创造的“比特侠”形象，并刊发比特币相关知识文章，以帮助儿童学习比特币知识。[2018/12/29]

说明：图4中的f,g对应图3中的f。即f,g是同一个多项式。其实只要是相同的值的集合，也可以不用于是同一个多项式。图3是一个特例而已。

跨多项式的校验

其实就是证明对于某个多项式f，g，存在两个点x,y，满足f(x)=g(y)。与存在两处不同：

多个多项式；不强制x,y的关系，即也可以等，也可以不等；有了(1)小节的基础，这次我们先看一下相关的定义：

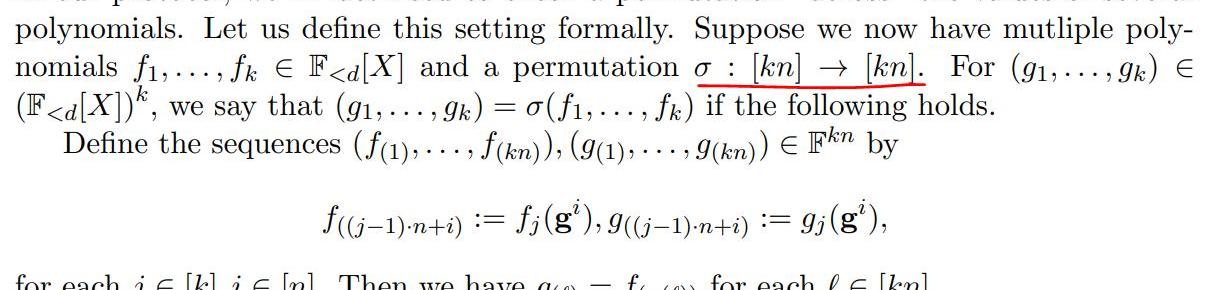
从定义可以看到，这次是两个多项式集合见的置换校验算法。从标注的部分可以看出：

两个多项式集合仍然具有相同的值的结合；为了区分集合里的多项式，自变量的索引得区分开来；因此，可以想象的到，如果存在两个多项式f,g，想要证明f(x)=g(y)，那么根据以上描述可以判断{f1,f2}={f,g}={g1,g2}。也保证了上述第1点的成立。

下面我们看一下具体的原理：

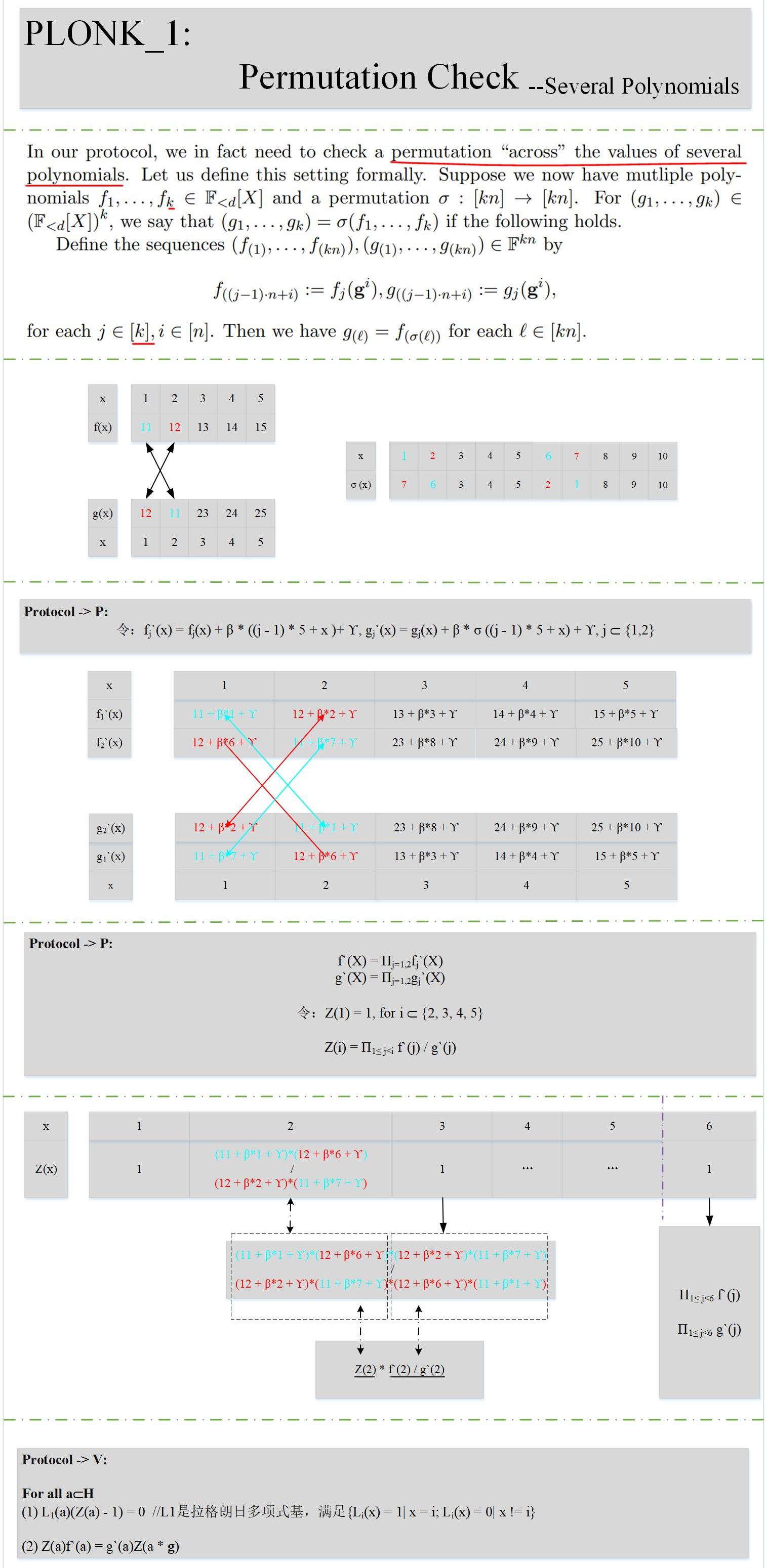
和(1)小节相比，证明方P增加了些工作量，验证方V工作量不变。结合上述描述，也能很容易的理解其数学原理。

说明：至此，其实我们已经慢慢的接触到PLONK算法的核心了，前面我们讲到，电路的满足性问题除了门的约束关系还有门之间的约束关系。

比如一个输入x，它既是一个乘法门的左输入，又是另外一个乘法门的右输入，这就需要去证明L(m)=R(n)，这就是跨多项式的置换校验。

下面再给出论文里的协议内容：

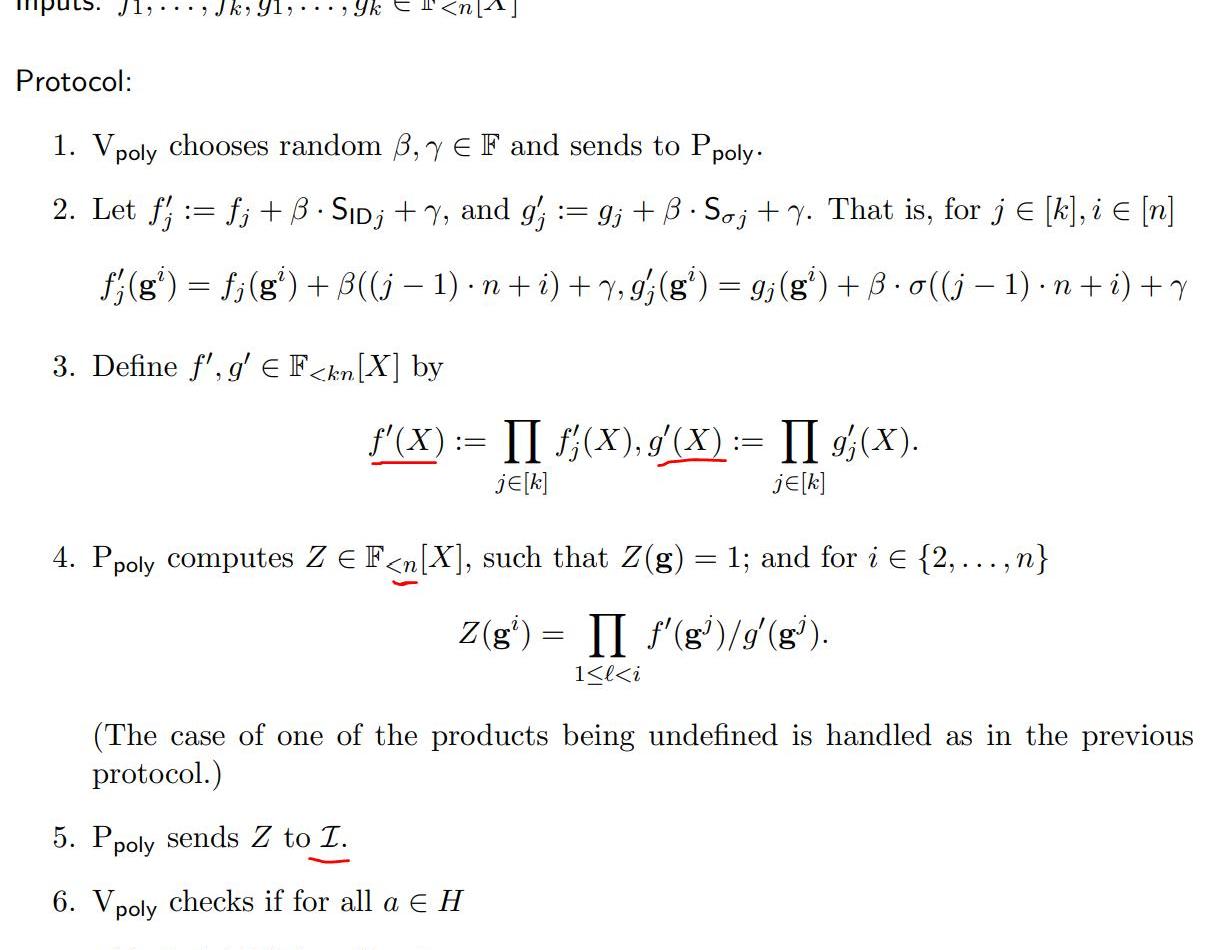
至此，本篇文章已经描述了，在PLONK算法里，电路的设计以及复制约束的成立验证两大部分，接下来，将会另起一片文章，去分享门约束的成立和整个协议的具体步骤。

以上都是作者小白的个人理解，还希望各位读者多多指教，谢谢。

标签：LONPLOARK比特币lon币最新消息UPLOAD价格Credmark比特币市值怎么算的

火必交易所热门资讯