DEFI:以太坊难度炸弹的爆发和拆除_Earn DeFi Coin

作者:?ThomasJayRush

翻译&校对:?曾汨&阿剑

来源：以太坊爱好者

每当以太坊的定时炸弹爆炸时，总会有两个问题出现在我们面前。第一个问题是：“什么时候出块会变慢，那简直不能忍。”第二个问题是，“这一次，我们应该将炸弹推迟多久？”

在这篇短文中，我为第二个问题提出了一个简单得微不足道的解答。难度炸弹应该被推迟多久呢？我的建议是：“给定需要在区块高度N处执行硬分叉，则将难度炸弹推迟N个区块。”

我并不打算在这篇文章中解释难度应该如何计算。下面这张图片在我的上一篇文章中已经出现过了，其中列出了难度的计算公式。

。在这种情况下，出块太快会导致难度增加，从而降低出块速度。如果10<=s<20，因子max(x)将变成0，从而确保当s接近目标时间14秒时，难度不再调整。而如果s>=20，因子max(x)的值将变成逐步减至-99，这会导致难度下降，从而提高出块速度。等式中的第二部分基于上一个区块的区块号。通过在指数中对100,000进行整除，创建出了一个以100,000个区块为周期的阶跃函数。第二部分也就是我们常说的难度炸弹。如果没有第二部分的话，难度炸弹便无从谈起。）

仔细观察这个公式，注意它由两部分组成。

公式的第一部分，我称之为“调整”。这一部分通过调整当前区块的难度来矫正上一个区块出块时间的偏差。这一调整要么降低难度，要么增加难度，这取决于生成上一个区块所花的时间。上图中第一个括号突出显示了这一部分。请花点时间搞清楚它的原理。A部分的实际效果与设计目标完全一致，它的作用是平抑哈希率的波动对网络运行的影响。从下文的图表中你可以清晰地看出计算公式中的A部分的作用完全符合预期。

数据：以太坊盈利地址占比创近5个月新高:1月22日消息，Glassnode数据显示，以太坊盈利地址占比为60.713%，为5个月最高值。[2023/1/22 11:26:05]

正因为A部分按照设计正常运作排除了哈希率带来的影响，所以我认为，在思考如何推迟定时炸弹时没必要考虑算力的实际规模。换言之，算力太低不会使难度炸弹爆炸时出块时间更长、算力太高也不能缓解难度炸弹的效果。鉴于以上分析，我的结论是，公式中的A部分与出块时间的减慢无关。而公式中的第二部分则是导致所有麻烦的罪魁祸首。

我接下来的分析会让你相信，完全可以将这两部分分开处理。这些分析使我们更容易看出A部分不会对出块产生影响，而B部分——炸弹——才会导致出块时间延长。除此以外，你还会知道拆除炸弹是多么地轻而易举，只需要在每一次分叉时简单地将时期重置为0即可。

生成数据并格式化

处理数据的第一步是获取数据。我们使用自己的软件库TrueBlocks编写了如下代码：

运行上面这段代码，可以生成以下这种非常简单的.csv格式的数据文件......

上面的数据再加上从EtherScan获取的每日哈希率列表，对于我们理解以太坊的难度计算来说已经绰绰有余了。我们使用了?RStudio?和一种名为“R”的数据编程语言来构建下文中的图表。如果你对“R”语言不太熟悉的话，强烈建议你去了解一下，这是一种非常出色的编程语言。

我们先来看一看以太坊的哈希率。

数据：以太坊活跃地址数达3个月低点:据Glassnode数据，以太坊活跃地址数（7d MA）刚刚达到3个月的低点，为30,656.185。[2021/6/13 23:34:09]

日均哈希率

第一张图表展示了以太坊主网的?日均哈希率，其中的数据来源于EtherScan。因为我不知道数据是怎么收集、创建出来的，因此无法保证这些数据的真实性，但我假定它是对的。可以点击这个链接查看相关数据。

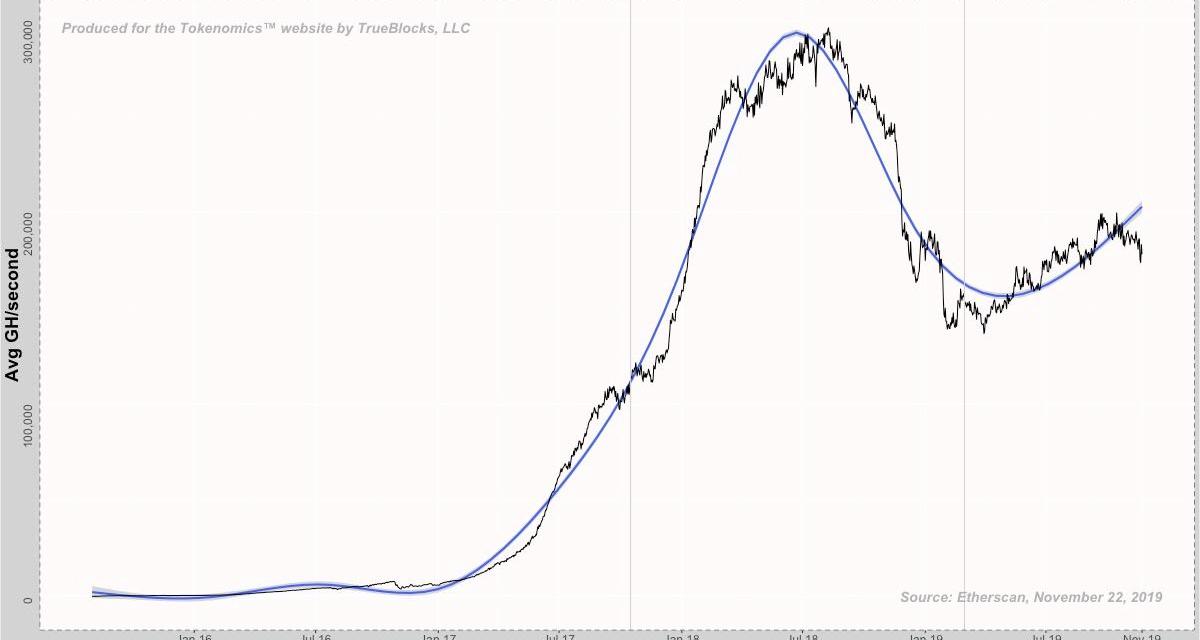
讨论：从上图中可以明显地看出，以太坊的哈希率随着以太币价格起伏而变化。这张图让我回想起了以太坊的价格走势。2017年夏，哈希率一路飙升，并在2018年第一季度达到顶峰。而2016年10月哈希率的起伏则是由于当时臭名昭著的DDos攻击，上图中两条灰色垂线代表的是两次硬分叉——即拜占庭硬分叉和君士坦丁堡硬分叉。这张图暂时就分析到这里，不过我们在接下来讨论区块链的难度数据时依然会提起它。

原始难度数据

第一张基于难度数据的图表展现了通过Parity的RPC调用?get_Block?返回的数据。首先，下面列出了一些标准的统计信息：

我们的第一张图表非常直观：

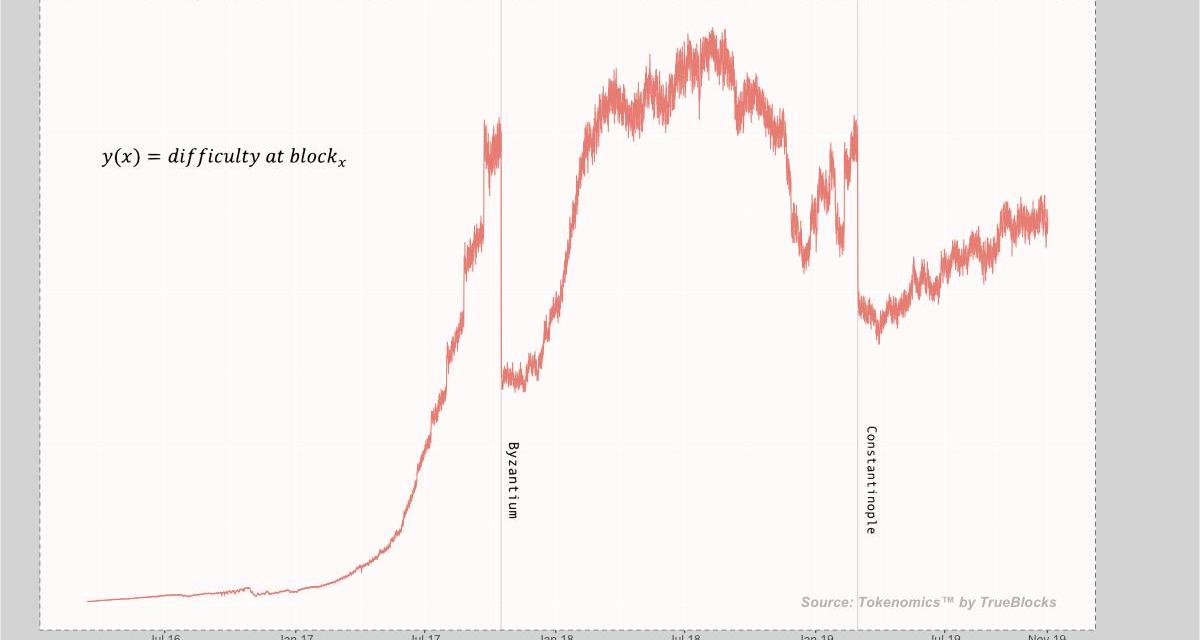
讨论：上图的数据是在第8,920,000个区块时生成的。尽管处理这么多数据记录对于“R”语言来说易如反掌，但考虑到数据挖掘的迭代性质，我们从每100条数据中抽取了1条记录作为样本，最终得到大约9,000条记录，并展现在上图中。与前文一致，上图中的灰色垂线也代表硬分叉。

独家｜当前以太坊建议Gas费用为84.28Gwei 环比下降16.19%:金色财经消息，据欧科云链OKLink链上数据显示，以太坊24h链上活跃地址数逾47.13万，环比上升2.99%；链上交易量近468.23万ETH，环比上升18.84%；链上交易笔数逾106.94万笔，环比下降1.78%。

截至下午2时，以太坊全网算力约为238.93TH/s，环比上升1.23TH/s，建议Gas费用为84.28Gwei，环比下降16.19%，未确认交易数约9.85万笔。[2020/9/24]

红线的高度代表给定区块时的难度值。你可以很容易地看出在每一次分叉时拆除难度炸弹的效果。请回看前文中关于哈希率的图表，在2016年秋天的DDos攻击中，你可以看到难度与哈希率之间的关系。

假如难度炸弹没有拆除——实际上从难度激活的那个高度开始把红线继续向上延伸——对于两次硬分叉都采取同样的操作，你会发现这与哈希率变化的图表惊人的一致。换句话说，哈希率和难度是紧密联系在一起的，这非常合理。因为这正是难度计算公式中的A部分设计的目的所在。它的存在就是为了直接根据不同的哈希率来调整难度值。

矿工的行为可能并不会因为难度炸弹的拆除而发生变化。他们的挖矿设备在难度炸弹拆除前后都同样地持续运行。唯一的改变是出块的平均时间变短了。

在我们进入下一张图表的分析之前，还有一些地方需要注意。请仔细看看拜占庭硬分叉前面的部分。你会发现难度水平上出现了4、5次单向的垂直跃升。事实上，每一次难度水平的跳跃幅度都是上一次的两倍。这些跳跃就是我们所说的难度炸弹。让我们一起把目光聚焦到图表的其它部分。

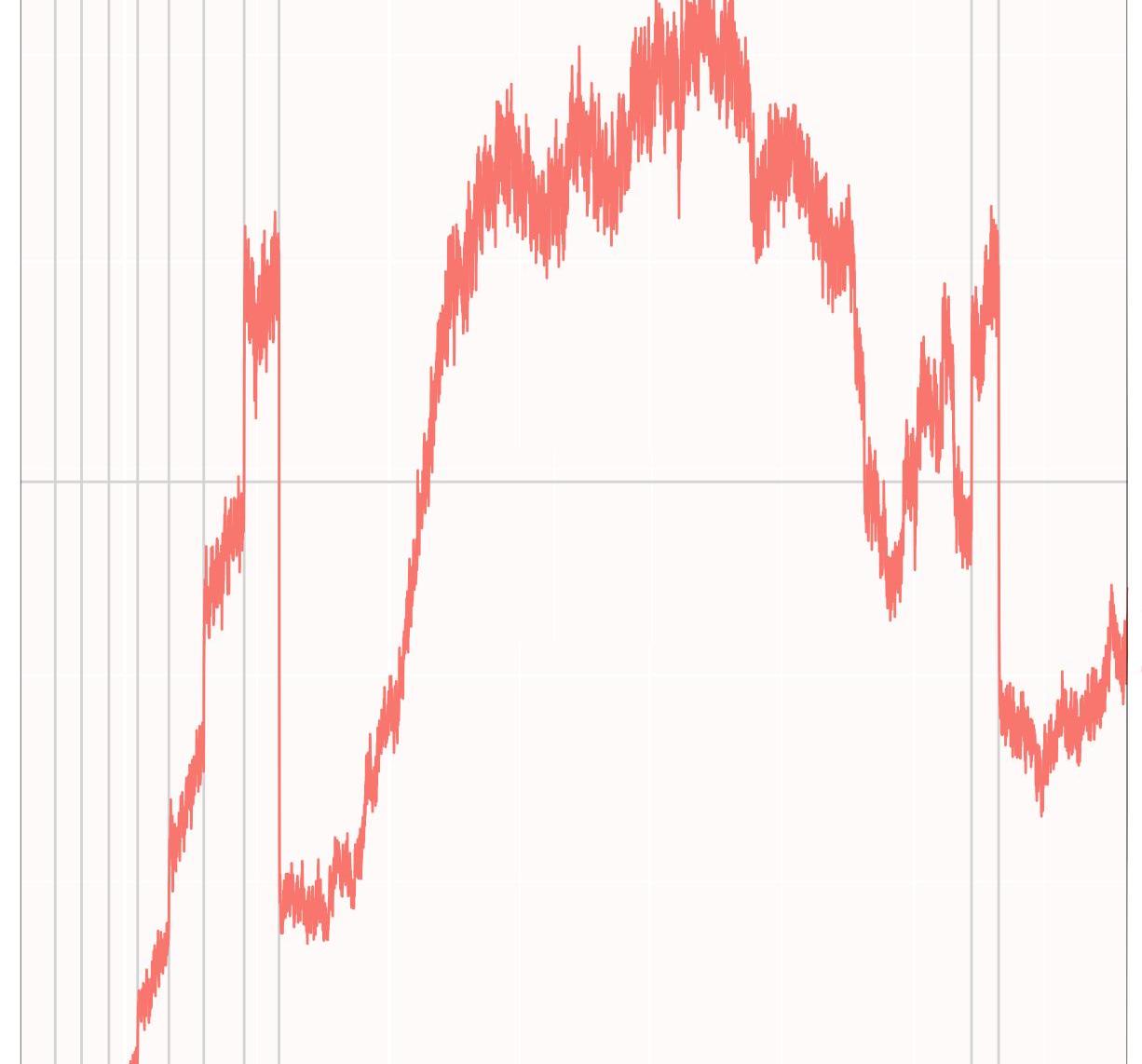
讨论：我们以100,000个区块为一组，用垂线将上图分隔开来。睁大你的眼睛，仔细看，代表难度跳跃的曲线跟我们作的垂线完全重合。在这些分隔线之间，难度持续上升，但上升速度远不及分隔线上的跃升幅度。难度的爆炸性增长与2017年时哈希率一路飙升的事实相一致。

数据：以太坊智能合约日发布量接近有史以来最高水平:9月14日消息，数据显示，目前每天有近300份智能合同在以太坊上发布，而两个月前只有50份左右。如图所示，9月9日，共有292份智能合约推出，仅比2018年7月创下的历史最高纪录少了一份。所有这些都表明，今年夏天使用以太坊的功能有了显著的增长。（Trustnodes）[2020/9/14]

也许你也注意到了每一次连续的“爆炸”——每次炸弹爆炸时的难度值的增量都是上一次的两倍。事实证明，这些跳跃的周期性对于理解当下正在发生的事情尤为重要。

在本文余下的图表中，我们的目标是将难度计算公式中的第一部分和第二部分分开。从而帮助我们更好地理解如何应对未来的难度炸弹。

每个区块的难度变化

在下一张图表中，我们来看看每个连续的区块之间的难度变化。其计算公式为y(x)=区块x的难度值—区块x-1的难度值。

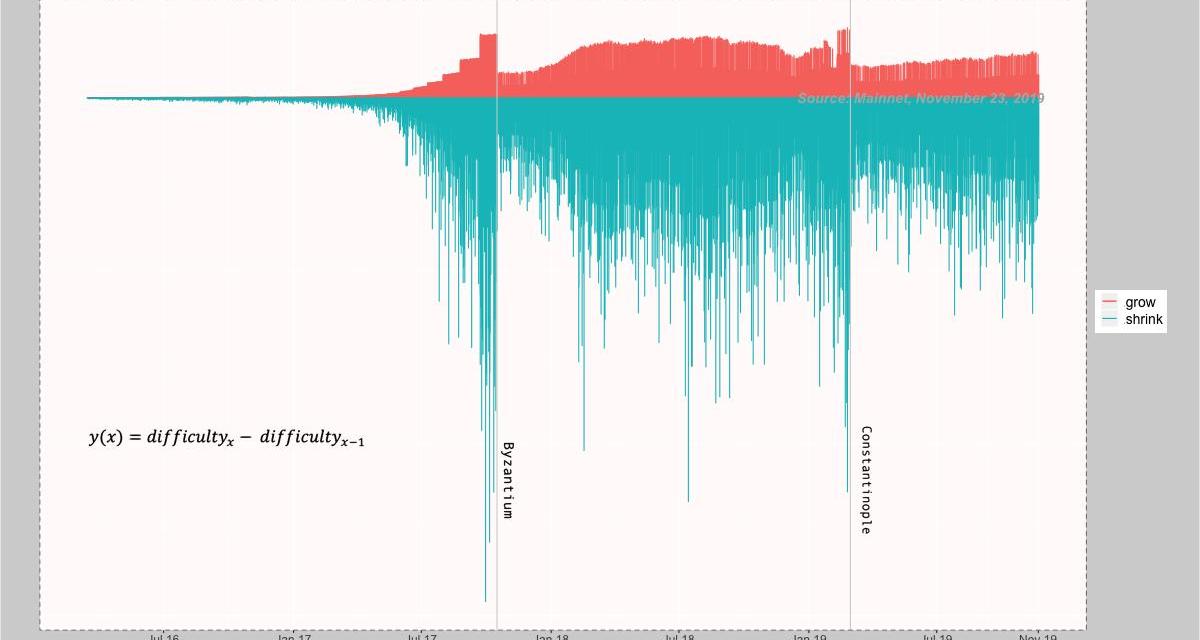
讨论：正如我们在上文提到的，A部分的计算使得难度在一个水平附近“徘徊”，以确保出块时间维持在14秒。上图通过使用红蓝色表示数据来揭示这种“徘徊”现象。图中的“增长”部分代表难度的正向变化。而图中的“收缩”部分代表难度的负向变化。难度始终围绕着0值“调整”。换句话说，这部分计算是为了维持出块时间的稳定，A部分的计算使得出块时间维持在一个稳定的值——14秒。

对你来说，这张图可能是你第一次看到难度炸弹的直观展现。很明显，每次爆炸时的难度都是上一次的两倍。

但在我看来，这张图表达的依旧不够清晰。举个例子，为何同样的图案在君士坦丁堡期间没有清晰地重现？其实是因为哈希率大大提高了。这部分计算可以使出块时间维持在14秒，但是系统的来回波动更加剧烈。这也解释了为什么我们无法在临近君士坦丁堡分叉时识别出难度炸弹，因为它被更加剧烈的波动掩盖了。

动态 | 以太坊ProgPoW审计资金获得批准:据coindesk报道，以太坊开发人员今天宣布，用于审计存在激烈争议的ProgPoW代码变更的资金已被批准。自2月份以来，开发人员一直在筹集资金以启动对ProgPoW代码的第三方审计。今天在每周一次的会议上，开发人员宣布已获得了目标金额50000 DAI（相当于大约5万美元） 。[2019/4/27]

那么，是否存在一些其它的措施，可以让我们看的更清楚呢？当然！这种办法确实存在，我们将在下一张图表中为你揭晓。

难度的相对变化

本文这部分的最后一张图表，展示了相对于区块总难度而言的难度变化百分比。计算公式为?y(x)=(区块x的难度值—区块x-1的难度值)/区块x-1的难度值。而上一张图表展示的是难度的原始变化。这张图表展示了标准化的难度变化，从而消除了算力增长带来的影响，我们从而可以更加清晰地看到难度计算公式中的两个不同部分——A部分与B部分。

下面是每个区块的难度相对变化图表：

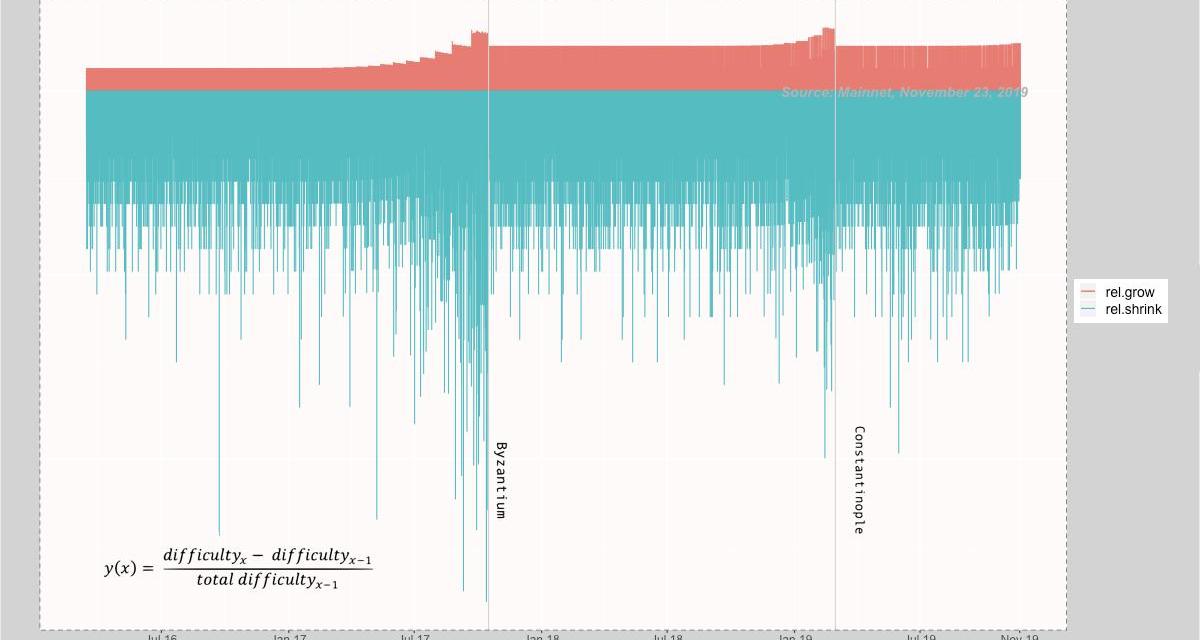
讨论：现在，你应该明白为什么我在前面中说在讨论难度炸弹时担心算力会适得其反得了吧。从这张图表中，你可以很清晰地看见，区块生产不受算力增加的影响，直到定时炸弹“抬头”。公式中的A部分使得出块的速度及产量维持在一个稳定的状态。在定时炸弹爆炸之前，难度几乎不受什么大的影响。

这里还有两件有趣的事情值得你注意：从上图中，你还可以看见炸弹在图表的最右侧开始“抬头”，尽管抬头的距离比起拜占庭和君士坦丁堡之间的距离要短得多——下文中我会解释这一现象；图表底部的条纹是因为计算公式里A部分中的对10整除的那部分而形成；更高的哈希率看上去好像会延迟“抬头”，正如LaneRettig在君士坦丁堡分叉之前提到的那样，我们在上面提到的文章中也写过。

关于这张图，我还有许多能继续分享的，也许哪天我会回过头来继续写。但接下来，我更想为在未来拆除炸弹提供更好的方法。

拆除炸弹的更佳方式

首先，我要再次强调，在担心定时炸弹的同时还担心算力波动会适得其反。计算公式中的A部分已经将算力增加的影响排除在外了。这也正是A部分存在的意义。平坦得近乎完美的难度增量证明了A部分的工作几近完美。很显然，哈希率对出块时间没有影响——但这一点我们已经知道了——这也是难度调整设计的目的所在。

炸弹由上述公式末尾的一个额外附加值所定义：

2^(floor(当前区块号/100,000)-2)

(译者注：floor(x)为向下取整函数，即取不大于x的最大整数，例如floor(3.14)=3）

上面的式子就是一个以2为底的幂函数。令?p=floor，我们可以将上面的式子改写为2p。最终，我们得到了一个以时段?p?为步长的阶跃函数。

不过，请记住，核心开发人员已经将炸弹重置了两次——没说错，就是“重置”的字面意思，他们重设了炸弹计算的周期起点。这是通过使用Go语言代码创建一个在计算中使用的伪块来实现的。目前来看，伪块在过去似乎起到了重置炸弹的效果。下图这张校正后的图表显示了这段时期的真实情况。

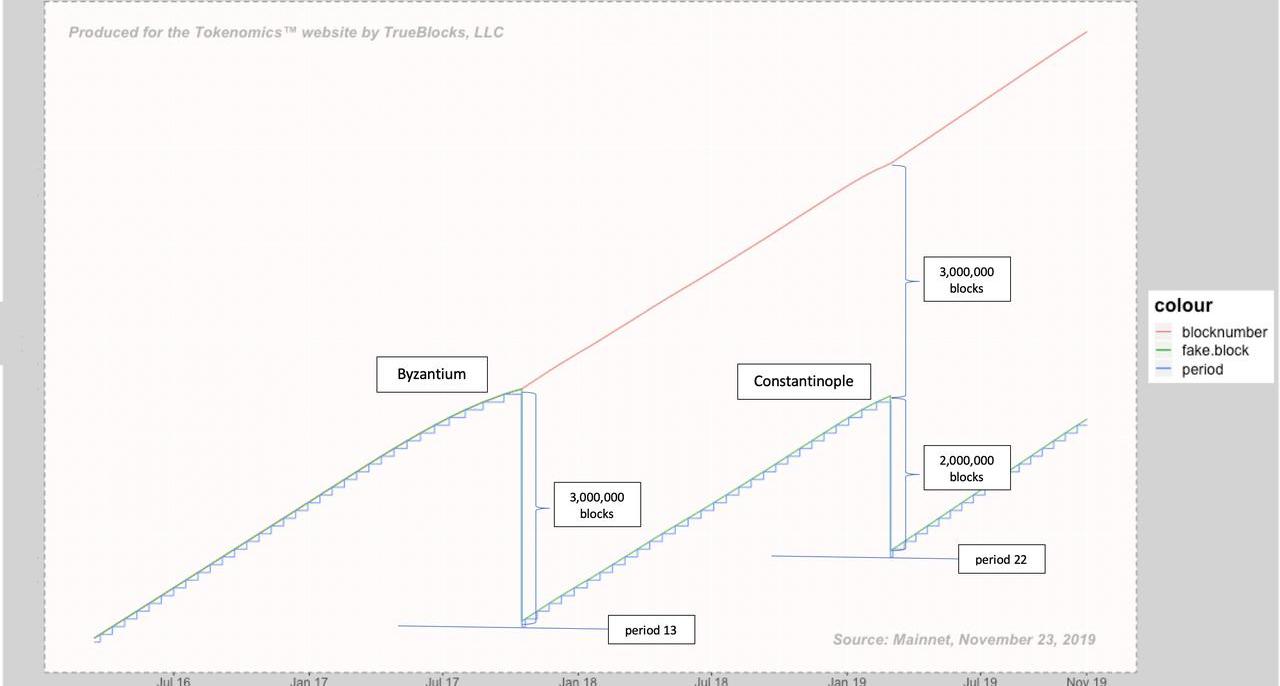
上图用红色来表示真实的区块号，其取值范围是0到8,920,000。而伪块号起初与红色的真实区块号重合，直到发生了拜占庭分叉，伪块号被重置到过去的3,000,000个区块。然后，伪块号与真块号平行增长，直到君士坦丁堡分叉，伪块号再次被重置。

下面这张表格中列出了重置后的一些信息，你发现什么奇怪的地方了么？

拜占庭分叉后的伪块号为1,370,000，将该值整除100,000可得时期为13。也就是说，在哈希率调整之后，每个区块的难度都额外增加了213?。而到君士坦丁堡硬分叉时，伪块号被重置为了2,280,000，也就是说时期变为了22，这意味着每个区块的难度额外增加了222。我想，这就是为什么定时炸弹爆炸得比我们预期中更早的原因。因为我们上次重置它时没有回退得足够远。

这次重置定时炸弹的建议值为回退69,000个区块，从而使得时期变为0。这才是需要重置的正确数量。

如何更好地重置定时的难度炸弹

每当我们必须重置定时炸弹时，有一种非常简单易行的方法将其重置为正确的值。通过这种方法，绝大部分和难度炸弹相关的问题将不复存在。只需要简单地将重置难度炸弹时回退的区块数设置成和分叉的FORK_BLOCK_NUMBER相同即可。通过这种方式，伪块号将被设置成接近0，时期也会变成0。

由于区块生产速度的减缓主要是因为定时炸弹的存在，因此通过上述方式，“抬头”效应将变得完全可预测。B部分的计算完全依赖于伪块号。如果我们在君士坦丁堡分叉时这么做，那么定时炸弹就不会爆炸得那么快了。

结论

非常感谢你能读到这里。我希望这篇文章可以引起那些对难度炸弹感兴趣的人的注意。我看到许多人都对难度计算问题感到困惑。在我看来，人们想的太复杂了。

以下是几个关于本文的简单总结：B部分的指数性质使得只有它与区块生产速度有关；计算公式中的A部分不会对出块造成有害影响，相反，它实际上起到了积极的作用；将时期或伪块重置为0有两个好处：允许最大限度地推迟定时炸弹，使得炸弹的重现变得非常可预测。

如果你对这篇文章有任何看法，请告诉我。希望我已经帮助大家理解了这些我烂熟于心的内容。

本文经作者授权EthFans翻译及再出版。

标签：DEFEFI比特币DEFIDecentralized Tower DefenseMEFI币如何把泰达币换成比特币Earn DeFi Coin

比特币价格今日行情热门资讯